Multimedia Learning in Games, Simulations, and Microworlds

Lloyd P. Rieber

The University of Georgia

Click here to access a PDF of a scanned copy of the original chapter.

This chapter reviews and critiques the scientific evidence and research methods studying the use of games, simulations, and microworlds as multimedia learning tools.   This chapter focuses on interactive educational multimedia, which is distinguished from scripted forms of educational multimedia by the degree to which users participate in and control the multimedia software. This chapter also uses the distinction between explanation and experience to understand the unique design opportunities of interactive educational multimedia.   The strongest empirical evidence comes from the simulation literature, especially that related to questions about how to design a simulation’s interface to provide feedback and questions about students engaged in discovery learning activities. Microworld research is less empirically rigorous with evidence continuing to remain largely anecdotal based on implementation reports.   Research on gaming is the most transitory, ranging from early research on learning from playing games to learning from designing games.   Current debates among educational researchers about what constitutes scientific research are particularly relevant to anyone interested in research about interactive multimedia due to the increased use of qualitative research methodologies and the newly emerging trend toward design experiments.            

What Is Multimedia Learning in Games, Simulations, and Microworlds?

            The purpose of this chapter is to review the scientific evidence on the use of games, simulations, and microworlds as multimedia learning tools. This is a tall order.   All three have very distinctive design and research pedigrees resulting in many cases from very distinctive philosophies about education.   Despite these differences, there are advantages to considering all three in discussions of interactive multimedia because each has strengths and ideas that help mitigate weaknesses or gaps often found in the other two (Rieber, 1992; 2003 for detailed discussions).

            This chapter is written to consider games, simulations, and microworlds within the broad organizational framework of educational multimedia.   Most of the educational multimedia studied by researchers is not interactive or experiential, but instead is used as part of instructional texts that explain content to students. For that reason, it is useful to consider the distinction between explanation and experience when trying to understand the design and use of educational multimedia. Multimedia that emphasizes explanation uses multimedia elements (e.g., text, static graphics, animation, and audio) in “scripted” ways. By scripted, I mean multimedia that is designed to be read or viewed in one particular way, similar to an encyclopedia article.   Consider a multimedia article about aerodynamics, such as that available at HowStuffWorks.com.   One section of the article involves text accompanied by an animation of the three-dimensional movements of a plane in flight.   The text and animation work together as coordinated elements of the explanation — one textual and one visual (animated).  

            In contrast, games, simulations, and microworlds are examples of interactive multimedia. The emphasis here is on experience made possible by dynamic elements that are under the user’s control.   Rather than read about flight, a flight simulator gives the user control over an animated plane with increasing levels of challenge. If goals are included, especially ones that encourage the user to take on another identity, such as a military pilot on an important mission, the simulation also becomes a game. Interestingly, text and static graphics may also be involved, such as providing the user (pilot) “just in time” information, such as weather forecasts, instructions for the mission, or directions from a simulated traffic controller.   The difference is that learning is based on the experience of flying the plane, rather than explanations about planes and flight.   Of course, both explanation and experience are important in education, but advocates of games, simulations, and microworlds put experience first with explanations serving a supporting role.

            The distinction between explanation and experience also highlights differences between different instructional and constructivist perspectives of education.  Although an examination of the epistemological differences between these perspectives is outside the scope of this chapter, this distinction is important because it serves as the basis for very different multimedia software designs. Microworlds were born out of constructivist thinking (Rieber, 2003), whereas simulation and gaming have long been aligned with more traditional instructional uses of educational software (Gredler, 1996, 2003). However, except for the most radical interpretations, constructivist perspectives do not ignore the role of instruction, but instead place greater emphasis on a person’s interaction in a content area and the relationship of that interaction to that person’s prior knowledge about the content (Jonassen, 1991).   Learning is believed to be achieved through active engagement with the teacher providing support, resources, and encouragement.   A constructivist perspective also places much emphasis on the social context of learning.  

            Current evidence suggests that technology has had little impact on education, despite the amount of money spent on it (Cuban, 2001; Cuban, Kirkpatrick, & Peck, 2001; Zhao & Frank, 2003).   In contrast, technology has had its most profound impact on learning outside of schools. Perhaps the closest relative to educational computing, due to its involvement of almost all children of school age, is video games (Gee, 2003).   It is interesting how the computer software business has competed for the opportunity to have children use their products in the education and gaming markets.   In education, the marketing is aimed at educators whereas in gaming the marketing is directly aimed at the children.   The amount of money spent on computer games is staggering, outpacing even that of the film industry (Poole, 2000).   Many adults, usually consisting of those who have never actually played a computer game, are quick to criticize the culture of computer gaming.   Computer gaming is largely viewed as a waste of time at best and an evil influence at worst, leading many to blame it as a significant cause of childhood violence.   The reality is far more complicated, and far more interesting, even from strictly an educational point of view.   Nevertheless, anyone wishing to understand the role of the computer within both educational and societal contexts must take interactive multimedia into account.

            I write this chapter from the point of view of an educational technologist, not a psychologist.   Despite this book’s goal of presenting “just the facts” as revealed by empirical research, I fear I am less confident than many of my coauthors about the robustness of the research evidence, especially when we move from the laboratory to the field.   The standards of scientific research in education has been the focus of much debate recently, especially since the release of the report Scientific Research in Education by the National Research Council (2002)(see Berliner, 2002; Erickson & Gutierrez, 2002 for examples of the debate; Feuer, Towne, & Shavelson, 2002). Generalization of the results from educational multimedia research to the “real world” of learning and performing in schools and the workplace should be viewed with considerable caution.   Researchers have just begun to seriously study educational multimedia, so the time is ripe is to question not only the results so far, but also the methods we have used.

What Is an Example of Multimedia in Games, Simulations, and Microworlds?

            I begin by presenting two software examples to show the similarities and differences between games, simulations, and microworlds. Both are examples that have been the basis of much research.   The first is a simple simulation that I designed for use in some of my own simulation research (see Rieber & Noah, 1997; Rieber, Noah, & Nolan, 1998).   It also includes a simple gaming feature.   The second example is a microworld called ThinkerTools (White, 1993; White & Frederiksen, 1998). The class of software referred to as microworlds is very diverse, so it is difficult to capture it with one example.   For example, many microworlds can be thought of as programming languages, such as Logo (Papert, 1980b) and Boxer (diSessa, 1997; diSessa, Abelson, & Ploger, 1991). However, ThinkerTools largely uses a graphical user interface allowing point-and-click methods to programming the computer.   Both ThinkerTools and the software I designed are designed to learn about simple mechanics, namely Newton’s laws of motion.   ThinkerTools also has interesting parallels to simulation and gaming, hence it is a good candidate to begin understanding how microworlds relate to them.

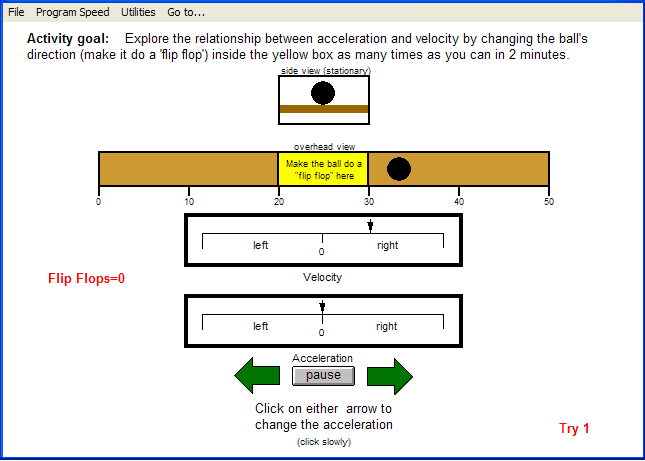
            Figure 1 shows an example of a simple simulation of Newton’s laws of motion, specifically the relationship between acceleration and velocity.   It also includes a gaming component.   If you are not familiar with the physics of acceleration and velocity, it’s important to know that each is a quantity specified by a magnitude and a direction   (such quantities are known as vectors).   Velocity is defined as the change in an object’s position over time; it consists of the speed and direction of an object.   Acceleration is defined as the change of the object’s velocity over time, implying again that the direction in which this change is occurring is important.   These two attributes, though very simple, often lead novices to confusion because their everyday encounters with the terms acceleration and velocity usually omit the idea of direction.   Most people understand and agree that a driver who guns the accelerator pedal accelerates the car.   But most nonphysicists have a hard time understanding that when slamming on the brakes the driver also accelerates in the opposite direction that the car is moving to bring the car to a quick stop. In this simulation, the user has direct control over the acceleration of a single object in the simulation — a ball.   The simulation begins with the ball moving at a constant speed from left to right.   Because the speed is constant, the acceleration is therefore zero.   If the user clicks once on the right arrow button, the ball experiences a small but continuous acceleration to the right, similar to holding down the gas pedal a wee bit and keeping it there.   Hence the ball’s speed to the right increases at a constant rate – the ball goes faster and faster.   If the user clicks on the right arrow again, the acceleration is increased and the ball’s speed increases at a slightly greater rate.   If the user then clicks on the left arrow twice, returning acceleration to zero, the ball’s motion returns to a constant speed, albeit increased over its initial speed, to the right.   If the user next clicks on the left arrow button, the acceleration of the object is to the left a slight amount.   What does acceleration to the left mean when the ball is moving to the right?   Simply that the ball slows down at a constant rate.   An interesting thing happens if the user does nothing further:   the ball slows down as it moves from left to right, eventually comes to a stop for just an instant, then starts moving right to left, slowly at first but then speeding up at the same rate that it slowed down.   This changing of directions is called a flip flop in this simulation, clearly a nontechnical term, but highly descriptive for the nonphysicists using the software.

Figure 1.   A snapshot of a computer screen during a simulation of the relationship between velocity and acceleration.   A user manipulates the ball’s acceleration by clicking on either large arrow.   This simulation also contains a game in which the user tries to change the direction of the ball while it is inside a yellow box (marked “make the ball do a ‘flip flop’ here”).

            As this example demonstrates, every computer simulation has an underlying mathematical model programmed into it that dictates how the simulation behaves.   The underlying model of this one happens to be based on Newton’s laws of motion. However, a simulation can be based on any quantitative model that can be programmed into the computer to an acceptable degree.   Scientific models are popular examples (e.g., physics, chemistry, biology, genetics) because the underlying models are more precisely defined than phenomena from other domains (e.g., sociology). When used for educational purposes, the students interact with the simulation to understand how this underlying model works.   Whether the underlying model is taught before, during, or after experiencing the simulation is a key design question for both instructional designers and educational researchers.  

            Much of my own research has explored some of the many decisions about how to design the simulation’s interface to help convey the underlying model to the user.   These are the decisions most relevant to the design of interactive multimedia. For example, as shown in Figure 1, this simulation encourages the user to imagine that the ball is moving on a very long board that can be tilted in either direction. This helps to contextualize the simulation for the user by providing a model case designed to help to make the essential concepts and principles underlying the simulation more salient.   For example, when the ball is moving at a constant rate it is equivalent to the board being flat (although this requires the user to understand and accept the idea that there is no friction generated between the ball and board that would slow the ball down).   The example described in the preceding text of the ball moving from left to right with the user then choosing to accelerate it to the left is equivalent to tilting the board downward to the left. The idea of a “tilting board” is conveyed by presenting a dynamic side-view graphic, which shows the tilt of the board when viewed on its side (as compared to the top-view graphic).   The goal of this tilting board model case is to help concretize the physics relationships at work here for users by tapping into their prior knowledge.

            It’s important to recognize that unless the instructor gives a student explicit directions or guidance, there appears to be no real purpose or goal to the simulation other than to explore it.   The ability of students to discover the underlying model through free exploration is a question explored by much research (e.g., de Jong & van Joolingen, 1998).   But how can the software be designed to provide an explicit goal to the student?   Typical school-based approaches including giving the student a question to answer or a problem to solve using the simulation as their “laboratory.”   Another way to accomplish this is with gaming.   The simulation shown in Figure 1 takes advantage of the flip flop concept mentioned previously to create a little game.   The goal of the game is make the ball do a flip flop anywhere inside the small yellow box.   When the student is successful, they get a point.   The yellow box then moves to another random location on the screen.   Obviously, the wider the yellow box, the easier the task. This points to a fundamental design characteristic of games — the challenge of the game should be proportional to the skill level of the user.   It is easy to program a computer game to increase the challenge as the user builds expertise.   In this case, the expertise can be measured by the time interval between scoring points.

            Is a game such as this an effective way to teach physics? Games are often touted for their motivational qualities.   If a game increases a participant’s enjoyment in the activity, they are likely to want to engage in and persist at the activity.   But, what other influences might the game have on learning?   From a cognitive processing perspective, a well-designed game might help focus a participant’s attention on critical aspects of the content or help the participant organize incoming information due to the presence of game goals and outcomes.   These questions were studied using the “flip flop in the yellow box” game described previously (Rieber & Noah, 1997).   Interestingly, the use of the game did have an effect on learning — a negative one.   Participants who were given the game actually scored significantly lower on the physics posttest than participants who were not given the game. However, all participants were also asked after each simulation trial to rate their overall enjoyment on a scale of 0 to 8 where 0 was “no enjoyment” and 8 was “extreme enjoyment.”   Participants who were given the game reported much greater levels of enjoyment than those who were not.   The quantitative phase of this study points to some interesting antagonism between negative effects of a game on learning and positive effects of the game on participants’ motivation.   But, the quantitative results could not answer why this was so. In a follow-up qualitative phase of the study, we learned that participants became obsessive with the game. In the parlance of gamers, they went into “twitch” mode and focused exclusively on improving their score in the game.   Due to this, they did not engage in reflection of their learning of physics.   Experience without reflection is detrimental to learning.   When engaged by the researcher to talk about the game’s relationship to physics, participants were able to make connections that aided their learning.

            In contrast to the simulation/game shown in Figure 1 there is a microworld called ThinkerTools shown in Figure 2.   With the ThinkerTools software, students can either build their own physical models of motion, or they can interact and modify prebuilt models that come with the software.   Unlike a simulation, the ThinkerTools microworld is best thought of as a “physics playground” offering literally unlimited ways to construct a physics model.   In this microworld, the user can add any number of objects, called dots that obey Newton’s laws of motion. However, the user can control the value of a large collection of parameters, such as each dot’s initial mass, elasticity (fragile or bouncy), and velocity.   Users can also determine other forces acting on the model, such as gravity.   Barriers and targets can be added to the model to add game-like designs.   The user can decide whether to directly control other forces on the dots, such as with the keyboard or a joystick, similar to a video game, or to just run the model to see what happens over time.

Figure 2.   A snapshot of the computer screen running ThinkerTools, a microworld of Newtonian mechanics. In this activity, the user controls the ball by pressing the left or right arrow keys.   Unlike a simulation, users can program their own activities and run their own experiments.

            What distinguishes ThinkerTools from the simulation described previously in this section is the amount of control the user has over the computer within the software.   It closely resembles computer programming, albeit confined within the boundaries of physics.   Users are limited only by their own creativity in determining what the ThinkerTools software is for or what it can do.   However, like other microworlds, ThinkerTools is also designed based on definite philosophical assumptions and ideals about learning.   The best uses of the tool, according to its designers, is to support an inquiry and modeling curriculum to empower students to develop metacognitive “knowledge about the nature of scientific laws and models, their knowledge about the process of modeling and inquiry, and their ability to monitor and reflect on these processes so they can improve them” (White & Frederiksen, 2000, p. 327).   Simulations and games can also be used in inquiry approaches, but they, unlike microworlds, usually mirror the intentions of their designers instead of the students who use them. The use and role of simulations and microworlds in education can also be distinguished, respectively, in terms of model using versus model building(Penner, 2000/2001).   Model using is where a student uses a model built by someone else, usually the teacher, in a learning activity.   Model building is where students are given access to the modeling or programming tool to build their own models.

What Do We Know About the Multimedia Learning in Games, Simulations, and Microworlds?

            Not surprisingly, the research on games, simulations, and microworlds is diverse, being based or motivated by very different pedagogical and philosophical approaches.   The research methodologies are equally diverse and include quantitative experimental designs, qualitative designs, and the newly emerging methods of design experiments.   In the following three sections, I examine some of the research on the educational use of simulations, microworlds, and games, respectively.  

Simulations

            This section reviews research related to the model using role of simulations in education — learning from a simulation designed by someone else. Two areas of research are discussed here.   The first deals with how characteristics of the simulation designed to represent the underlying model are perceived and used by students while interacting with the simulation. Much of this research asks questions similar to other multimedia research efforts, such as the role, influence, or effects of different representational elements of the simulation on learning.   An example would be examining the use of graphic or text for key elements of the simulation’s interface, such as how the simulation provides feedback based on user actions or choices while operating the simulation.   The second area of research examines students’ scientific discovery learning with a simulation. This research concerns the degree to which students are able to discover and understand the simulation’s underlying model on their own versus the degree to which they need varying levels of instructional support or guidance.

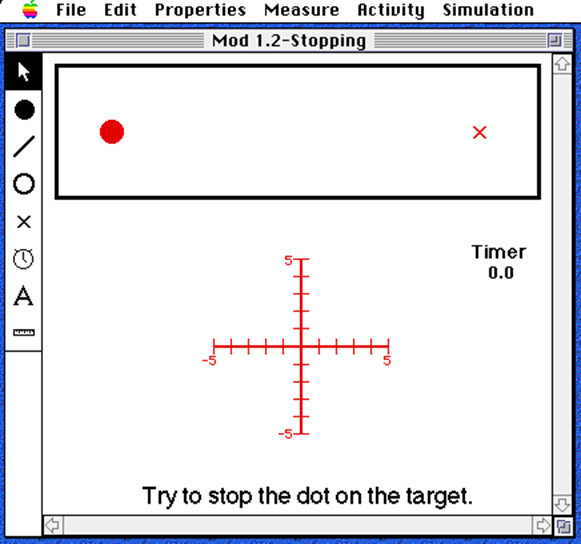
            A good example of research investigating how different representations influence learning from simulations is a series of studies I conducted with colleagues (Rieber, 1990, 1991, 1996a; Rieber, Boyce, & Assad, 1990; Rieber & Kini, 1995; Rieber & Noah, 1997; Rieber et al., 1998; Rieber & Parmley, 1995; Rieber et al., 1996; Rieber, Tzeng, & Tribble, in press).   In this research, we examined the role of computer animation as graphical feedback during a simulation.   When interacting with a simulation, a user must first be able to tell the difference between their goals and intentions, then be able to judge whether or not their intentions have been met.   Norman (2002) refers to the differences in these two states as the gulfs of execution and evaluation, core principles of interface design.   The typical method we used in this research was to design three versions of a physics simulation (similar to that shown in Figure 1) that varied in the way feedback was presented to users as they interacted with the simulation:   animated graphical feedback, textual feedback, or a combination of both graphical and textual feedback. Similar to a video game, if the user wanted an object to move to the left, he or she would press a screen button that applied force to the object in the left-hand direction. An example of a simulation designed only with textual feedback is shown in Figure 3.   Feedback is presented solely through the use of numeric readouts that depict the current position of the object being manipulated and, in the case of Figure 3, the position of a target that participants are trying to hit with their object.   Both the graphical and text-based simulations use exactly the same underlying model.   The only difference is the way the feedback is presented to students. We evaluated learning in both explicit and implicit ways.   Explicit learning was measured using a traditional multiple-choice test of physics understanding, whereas implicit learning was measured by the ability of students to complete a game-like activity similar to the simulation.   In most of our research, we used a scientific discovery approach, that is, we deliberately did not include physics instruction to accompany the simulation.   We wanted to be sure that all learning occurred solely through interaction with the simulation.

Figure 3.   A snapshot of the computer screen running a simulation/game of Newtonian mechanics where all feedback is given to the user in numeric form.

            As it turns out, this type of learning is very difficult for students who are novices in physics. One prediction is that animated graphical feedback would be a better way to represent information and relationships for Newtonian mechanics — animated balls are close analogs to actual moving balls.   However, such representations may not make the relationships explicit, that is, learning might remain implicit in the simulation activity unless the person makes a deliberate effort to “translate” the relationship into the verbal terms needed to answer the posttest questions.   A person given the textual feedback who is successful at the simulation would have to work hard to make such a translation, thus leading to the prediction that textual feedback would lead to more explicit learning, especially when measured with verbally stated multiple-choice questions.

            When participants used the simulation in a discovery-oriented way, that is, without any accompanying instruction, results sometimes, but not always, favored the use of graphical feedback over textual feedback or graphical plus textual feedback on tests of explicit learning, such as traditional text-based questions (Rieber, 1996a; Rieber et al., 1996).   In contrast, graphical feedback led to superior performance on tests of implicit learning (computer game-like tasks).   In other words, graphical feedback was more beneficial than textual feedback for implicit, or near-transfer, tasks.   Yet, on explicit, or far-transfer, tasks requiring students to translate graphical symbols into verbal symbols, the difference was not as compelling.

            What is needed to further help students explicitly learn the physics principles well enough to answer verbally presented problems?   In follow-up qualitative studies where we interviewed participants as they used the simulation, we noticed that few people discovered the “secrets” of the laws of motion without some help or guidance by the interviewer.   The guidance was not complex or time consuming— just pointing out some critical features to the participant based on their experiences or simple questions that helped them to focus on key physical principles.   The guidance did not even interrupt their interactions with the simulation, but instead seemed to give them insights for their subsequent attempts.   What was needed was guiding information — an explanation – to be given at just the right time.

            In a follow-up research study we included the use of short, embedded multimedia explanations (with both text and animation) of the physics principles and showed them to participants during the simulation (Rieber et al., 2004).   Providing these short explanations made a huge difference.   Participants given graphical feedback far outperformed those given textual feedback, but only when accompanied by the short explanations.   We think providing the explanations intermittently while using the simulation helps students to organize their experiences with the simulation, helping them to construct appropriate mental representations of the physics content.   In contrast to full-blown tutorials that divide explanation and experience, the short explanations provide just the right amount of explanation at just the right time.   Another interesting result emerged from our qualitative research on these simulations.   Those participants who did master the simulation shifted their preference from the graphical feedback to the textual feedback.   They did so for several reasons.   The first was motivational — they were looking for a greater challenge.   The second was tactical — as they began to develop strategies based on emerging mental models of the physics principles, textual feedback became more aligned with those strategies.   For example, an implication of Newton’s second law is the idea that when forces acting on an object in one dimension are balanced from either direction, the object stops moving in that direction.   When participants understood this principle and began using it as one of their strategies for controlling the motion of the ball, it became easier for participants to use textual feedback that displayed the total accumulated force in numerical terms.

            We also measured the frustration levels of participants by asking students throughout the research (right after each simulation trial) to report their current level of frustration on a scale of 0 to 8 where 0 was “no frustration” and 8 was “extreme frustration.”    Participants given only textual feedback consistently reported much greater frustration than those given graphical feedback.   This is not surprising because the mental effort in converting the numerical feedback into a spatial position on the screen is hard work.

            The second area of simulation research reviewed here is that dealing with scientific discovery learning.   The purpose of this research is to understand the process students go through to understand a simulation’s underlying model in the absence of explicit instruction about the model. This research focuses on inquiry learning by students, as they use scientific reasoning to solve problems with the simulation. One of the most thorough reviews of this research is provided by de Jong and van Joolingen (1998).   Their review demonstrates how difficult it is for students to use simulations in this way.   For example, students are often prone to confirmation bias, the tendency to design experiments that will lead them to confirm early formed hypotheses.   Students find it difficult to discard hypotheses, even when faced with contradicting data.   Similarly, students find it difficult to construct hypotheses that can be easily tested with experiments.   Students have difficulty in setting up an appropriate experiment to test even a well-stated hypothesis.   Of the many conclusions offered by de Jong and van Joolingen, one is similar to that already discussed:   information, guidance, or instructional support needs to be provided while students are using the simulation, as compared to extensive instructional treatments prior to using the simulation.

            Another conclusion is that students benefit from simulations that progressively become more difficult and complex, doing so only as students gain expertise with earlier and simpler skills. de Jong and van Joolingen (1998) refer to this as the technique of model progression.   A good example of this technique is research by Rieber and Parmley (1995).   In this study, adult participants were given either a structured simulation on the laws of motion based on the model progression technique, or the full simulation.   The structured simulation consisted of four activities, each of which included a controlled number of new subskills.   Each successive activity incorporated the subskills from the preceding activity.   In addition, half of the participants were given an explanative tutorial of this content and half were not.    Results showed that participants given the structured simulation without the tutorial learned as much as other participants given the tutorial.   In other words, explanations were not necessary when participants were given a carefully structured experiential approach.   Interestingly, participants given the structured simulation without the tutorial reported less confidence about their answers to the posttest questions than participants who were given only the tutorial — learning without formal instruction was outside of their comfort zone.   The purpose of this kind of research is not to advocate withholding instruction from students, but rather to gain a better understanding of when instruction is either unnecessary or most needed.

Microworlds

            A microworld is an example of an exploratory learning environment (diSessa, Hoyles, Noss, & Edwards, 1995).   The most well-known and studied microworlds include Logo (Papert, 1980b), StarLogo (Resnick, 1994), Boxer (diSessa & Abelson, 1986; diSessa et al., 1991), ThinkerTools (White, 1993; White & Horowitz, 1987), SimCalc (Roschelle, Kaput, & Stroup, 2000), Geometer’s Sketechpad (Olive, 1998), and GenScope (Horwitz, 1999).   Although different conceptions of microworlds exist, three goals are common to all. First, they offer a way for more people, starting at a younger age, to understand and explore concepts and principles underlying complex systems.   Second, microworlds focus primarily on qualitative understanding based on building and using concrete models.   Third, there is a deliberate attempt to reduce the distinction between learning science and doing science.   Indeed, the goal is to have students use technology in ways similar to those of a scientist.   Although the concept of a computer-based microworld can be traced back at least as far as Seymour Papert (1980a), a contemporary definition comes from Andy diSessa (2000):

            A microworld is a genre of computational document aimed at embedding important ideas in a form that students can readily explore. The best microworlds have an easy-to-understand set of operations that students can use to engage tasks of value to them, and in doing so, they come to understanding powerful underlying principles. You might come to understand ecology, for example, by building your own little creatures that compete with and are dependent on each other (p. 47).

            Microworlds can be described by both their structural and functional affordances.   Structurally, microworlds consist of the following (Edwards, 1995):   a) a collection of computational objects that model the mathematical or physical properties of the domain; b) links to multiple representations of the underlying model; c) opportunities or means to combine the computational objects in complex ways; and d) inherent activities or challenges for the student to explore or solve in the domain.   A functional analysis of a microworld focuses on the interaction between the student, the software, and the setting in which it is used.   Students must be able to know how to use a microworld and want to use it.   In other words, a microworld needs to match both the cognitive and affective states of the user. Students learn about a domain through exploration with the microworld.

            Research on microworlds in education has been contentious.   Early research in the 1980s was focused on studying the effects of Logo on children’s learning (e.g., Clements & Gullo, 1984; Pea & Kurland, 1984).   However, Papert (1987) felt such research studies missed the point:

Papert took the view that Logo would be used by children to explore and learn mathematics as naturally as they learned language.   However, several interesting research programs that began in the 1980s began to show the need for some imposed structure and designed activities in order for students to learn with microworlds. The work of Barbara White is a good example, beginning with her dissertation on dynaturtles (White, 1984) that led to the development of the ThinkerTools software and curriculum (White, 1992, 1993; White & Frederiksen, 1998, 2000; White & Horowitz, 1987; White & Schwarz, 1999).   Although White’s early research and others (e.g., Harel & Papert, 1990, 1991) used traditional quantitative and qualitative methodologies, others have used a methodology now best known as design experiments(Brown, 1992; Cobb, Confrey, diSessa, Lehrer, & Schauble, 2003; Collins, 1999; Newman, 1990; Richey & Nelson, 1996).   A good example of this is research done with the SimCalc Project, an effort designed to give children opportunities to learn about the mathematics of change and variation, such as calculus (Roschelle & Jackiw, 2000; Roschelle et al., 2000).

            A design experiment couples formative evaluation’s aim of successively improving an innovation’s design by studying its use in practice (see Dick, Carey, & Carey, 2001) with the scientific aims of theory building and theory testing (Cobb et al., 2003) . A design experiment sets a specific pedagogical goal at the beginning and then seeks to determine the necessary organization, strategies, and technological support necessary to reach the goal (Brown, 1992; Collins, 1999; Newman, 1990, 1992) . Such experiments involve an iterative and self-correcting process that resolves problems as they occur. The process is documented to show what path was taken to achieve the goal, what problems were encountered, and how they were handled. Unlike traditional experimental or case-based research, design experiments offer the ability for a researcher to show the evolution of an innovation’s design, implementation, and use, rather than just focus on the results that come at the end of the design cycle.  

Gaming

Similar to model using versus model building, using games in education as a route to learning can be conceptualized two ways: playing educational games designed by others or designing your own game.   The research literature focusing on whether playing games leads to learning (gains in achievement) is mixed (Kirriemuir & McFarlane, 2004).   When games are compared to traditional classroom instruction (the most common research method), few differences in learning are reported (Dempsey, Lucassen, Gilley, & Rasmussen, 1993-1994; Gredler, 2003; Randel, Morris, Wetzel, & Whitehill, 1992).

Another approach to studying gaming is what can students learn from designing their own games.   A good example of this research on gaming comes from the work of Yasmin Kafai (1994; 1995; Kafai & Harel, 1991). Their research has focused on student motivation and learning while building multimedia projects.   In these “children as designers” studies, elementary school students are typically given the task of designing an educational game for a younger audience (i.e., fifth graders designing for third graders).   In one example (Kafai, Ching, & Marshall, 1997), qualitative results showed how students used the design activity as an opportunity to engage in content-related discussions.   Quantitative results also demonstrated increased learning of astronomy concepts by students.

For almost a decade I and many of my graduate students have spent time with elementary and middle school students designing and developing educational computer games (Rieber, Luke, & Smith, 1998). The motivation for starting the project was based on a simple question:   Would children be able to take advantage of the opportunity to engage in game design when properly supported to do so?   The purpose of our research was to observe the social dynamics of children working collaboratively in teams.   Besides the qualitative data produced from our observations, our other primary measure was whether or not the children produced a working game.   If so, the game became an artifact for research by giving us insights into how children find ways to put subject matter they were learning in school to use in a context that they value (i.e., games).   The children designed the games’ goals, rules, characters, and graphics.  

One research study (Rieber, Davis, Matzko, & Grant, 2001) we conducted focused on the following questions: 1) would children, other then those who designed the game, find these games motivating to play; and 2) based on the children’s own play behavior, what features of these noncommercial games do children report as exemplary and noteworthy? To answer these questions, we gave students in two classrooms (30 students in all) the opportunity to play games designed by other students over a period of three weeks.   As students chose to play the games, the computer also logged data about the children’s playing behavior (which game played, how often, and for how long).   The children were also asked to rate the games throughout the three-week period.   We tracked the students’ rating patterns over the course of the study.   These quantitative data, in combination with follow-up interviews with 12 of the 30 participants, yielded interesting outcomes.   First, the children’s ratings consistently matched their game-playing behavior.   That is, the games they chose to play most frequently and for the longest periods were also the games they rated most favorably.   The children’s ratings were also stable and consistent over time.   They came to form opinions about the games quickly and their opinions did not change much over time.   Three game characteristics favored by children included: 1) the quality of the game’s storyline; 2) competition; and 3) appropriate challenge.   These characteristics are consistent with much of the game-design literature.   However, unlike the game-design literature, two other game characteristics did not matter much to the children:   1) the game’s production values; and 2) the integration of the educational content with the game.

What Are the Limitations of Research on Multimedia Learning in Games, Simulations, and Microworlds?

            Research on multimedia learning in games, simulations, and microworlds has used a diverse collection of research methods with equally divergent results.   There is no one “right” approach.   As any student of educational research knows, quantitative experimental research generally has strong internal validity, but weak external validity, whereas it is just the opposite for qualitative research. Experimental research based on randomized trials is often touted as the “gold standard” of scientific research (National Research Council, 2002) . The strength of an experimental design is the ability to study one variable at a time while controlling all others in order to understand how much influence the variable has on learning.   However, experimental research comes with the inherent criticism that the results reflect little on how learning actually occurs in the messy world of classrooms and homes.   In contrast, qualitative designs yield interesting glimpses into particular cases, but run the risk of leading researchers astray if the small sample sizes are not representative of the target audience.   Furthermore, qualitative research poses a constant risk that a researcher’s bias for or against the innovative might “leak into” their interpretation.

            For these reasons, the best advice is to advocate for mixed methods when studying interactive multimedia (see Johnson & Onwuegbuzie, 2004).   Quantitative designs yielding answers to “what?” and “when?” research questions using data from large numbers of participants can be balanced with the strength of qualitative designs focusing on “why?” questions with small numbers of participants.   A good example of the value of mixed methods is the study by Rieber and Noah (1997) .   The quantitative results showed no differences in the use of a visual metaphor in learning physics.   However, in the qualitative stage of the research where we sat down and observed participants individually as they used the simulation, it was clear that participants used and processed the visual metaphor in very productive ways.   They tried to understand the metaphor and, most importantly, tried to use it as a cognitive tool for understanding the physics.   Why did our quantitative results not reveal something?   It’s most likely the quantitative instruments (e.g., multiple-choice posttest) were not sensitive to the kinds of cognitive processing actually triggered by the visual metaphor.  

            The study of interactive multimedia presents unusual problems and opportunities for researchers. Multimedia research is prone to many sources of confounding, one of the most significant is the nature of the innovation used in the research.   A simulation, game, or microworld that is poorly designed or implemented leads to erroneous results that many researchers may find difficult to notice.   Interactive multimedia cannot be viewed merely as part of the “apparatus” of psychological research.   Instead, they are believed to work with people as “partners” in the learning process (Salomon, Perkins, & Globerson, 1991) by acting as “cognitive tools” (Lajoie, 2000; Lajoie & Derry, 1993) . As a result, research designs must be creative in understanding this partnership, especially because the design of the innovation is usually in a state of flux. As previously mentioned, one of the most promising research methodologies for the study of interactive multimedia is the design experiment.

What are some of the Implications of the Research for Cognitive Theory?

            Given the richness of interactive software such as simulations, microworlds, and games, there are many theoretical perspectives one can use in trying to understand their role in learning and cognition.   Only two will be reviewed here:   Dual coding theory and mental models. Other relevant theories include activity theory (Barab, Evans, & Baek, 2003; Jonassen & Rohrer-Murphy, 1999) and Play Theory (Pellegrini, 1995; Rieber, 1996b; Sutton-Smith, 1997).

            When viewed from the point of view of message design, the focus is on the way in which information is represented.   Paivio’s dual coding theory has been used extensively to demonstrate the well-known picture superiority effect for memory tasks (Paivio, 1990, 1991; Sadoski & Paivio, 2001). Although adaptations of dual coding theory exist (e.g., Mayer, 2001), dual coding theory remains well suited to explain learning from multimedia. In my own work, I’ve tried to extend dual coding theory to include a user’s dynamic interactions with a simulation.   A brief overview of the theory is in order.

            Dual coding theory divides cognition into two processing systems, one verbal (or semantic) and the other nonverbal.   For the purpose of this discussion, the nonverbal system is best understood as a visual system.   Dual coding theory predicts three levels of processing within the verbal and visual systems — representational, associative, and referential.   Representational processing describes the connections between incoming messages from the environment and either the verbal or visual system.   For example, hearing the word tree, a verbal message, would trigger the verbal system whereas looking at a picture of a tree would trigger the visual system.   Associative processing is when informational units within either of the systems are activated.   Dual coding theory predicts different hierarchical organizations within each system.   The verbal system is considered as sequential or linear, whereas processing in the visual system is considered synchronous.   For example, the memorization of a poem is stored within the verbal system such that one cannot easily scan memory to the third line; one would have to start from the beginning to get to the desired line of the poem in memory.   In contrast, a person who has stored the image of a familiar place, such as one’s work place, can easily imagine the place from any point and then mentally scan left or right.   The final type of processing, referential, builds connections between the verbal and visual system.   Simply put, this is defined as an image stored in the visual system being linked to a linguistic unit in the verbal system.   A person who looks at a picture of a parent (visual system) can quickly state the parent’s first name (verbal system) because the two bits of information are linked.  

            In general, then, we should be interested in how to dually code information because there are obvious advantages to having two routes to retrieving information from memory.   But interactive software goes beyond mere recall of stored information in long-term memory.   Learning with a simulation focuses much attention on identifying and using relationships being modeled in the simulation.   The distinction between explanations and experience again is useful here.   One can use dual coding theory to predict that the verbal system is more apt to store explanatory accounts of conceptual relationships, whereas the visual system should be more suited to handle the experiential.   When designed well, a user has many opportunities to build strong referential connections between both explanatory and experiential representations of the concepts and principles being modeled in the simulation.   Two essential ingredients for forming these relationships are time to reflect on the relationships and guidance to test one’s understanding.

            The second theoretical framework — mental models— is particularly useful for explaining learning with simulations and microworlds.   A mental model is one’s “personal theory” of some domain or environment (Gentner & Stevens, 1983; Jih & Reeves, 1992; Mayer, 1989).   The word theory may be too strong here in that a mental model is believed to be loosely organized and open to continual refinement.   Everyone forms mental models to help predict the systems we confront in our environment, such as our home heating systems, refrigerators, or automobiles.   For example, I grew up without whole-house air conditioning. When I was a young boy, I always wondered why we just didn’t leave our refrigerator door open to cool the house. My mental model of a refrigerator was that of a device that “created” cold air. It wasn’t until I got older that I developed a more refined mental model of the refrigerator transferring heat from the inside to the outside, thus making it clearer how important it was for the refrigerator’s door to be closed.   Of course, a physicist has a much more sophisticated mental model based on the laws of thermodynamics.

            Working with a computer is another good mental model example to explore, although here we have an example of where the manufacturer tries to help us by giving us a mental model, that of a desktop.   Of course, there really aren’t little yellow folders stored in our computers, but this model helps us to predict how the computer system operates so we can use it. A desktop is a good example of a design device called a conceptual model (Norman, 2002). Simulations can obviously be built with similar conceptual models to help users understand what the simulation is modeling.   Microworlds go one step further by allowing a user to build their own models, thus their creations become external artifacts of one’s mental models.

What Are the Implications of the Research for Instructional Design?

            Among the most important conclusions I draw from the research with simulations is the complex relationship between experience (during a simulation) and the nature and timing of explanations. As already discussed, it is very difficult learning from simulations in a discovery-oriented design, even though the potential for deeper levels of processing continue to make this an attractive area for design.   Constructivist perspectives generally favor more open-ended learning environments over instruction-directed environments, yet the research consistently points to the need to give students some structure.   Is there a way to provide structure without subverting the exploration and discovery process? The question of whether the teacher should coach, counsel, or teach will likely remain contentious for some time. The study by (Rieber et al., 2004) suggests an appropriate role for how explanations should be situated in a simulation.   Although explanations were embedded directly into the simulation, one would predict a teacher or more capable peer should be able to offer much richer and more meaningful explanations than the few studied in this research. But the point deserves restating that short explanations seem to work best when offered at the right time during the simulation experience. Another promising strategy is to design the simulation to become progressively more difficult only after the learner masters earlier skills (i.e., model progression).

What Are Some Productive Future Directions for Research?

            Much of the experimental quantitative research on interactive multimedia has been conducted over very short intervals.   The average duration that participants interact with a simulation in my own research is about 90 minutes. Other simulation and gaming experimental research have participants interact with the materials for several sessions and several weeks.   For a controlled experiment, the more time the research takes, the greater the likelihood that confounding factors will increase.   In contrast, researchers of microworlds tend to also be the developers.   They spend significant time with participants, such as elementary, middle, or high school students and their teachers over many months.   But, the research that is generated is open to much criticism; it is largely anecdotal based on observation that is not held to rigorous qualitative methods.   There are exceptions, such as the ThinkerTools research and other isolated examples (e.g., Harel & Papert, 1991).

            I believe the most productive future direction of research in interactive multimedia will come from the combination of mixed methods and design research approaches. Design research is in a very formative period.   Much of what is offered as design research now lacks scientific rigor and is instead based on anecdotal observations, often times heavily biased toward the innovation.   However, design research based on strong and rigorous data collection methods and theory generation offers great promise in explicating those features of interactive multimedia most effective for learning based on a series of design iterations.   In other words, rather than giving the results of a study, design research tells the complete story of what revisions were needed, what revisions were made, and how those revisions collectively related to learning.   Interestingly, design research is not necessarily aligned with either quantitative or qualitative methods, but draws well upon both.   Design research lends itself to research teams, which should increase the likelihood of involving researchers with methodological skills encompassing both qualitative and quantitative areas.

Glossary

Educational game.   Competitive rule-based activities involving one or more players with an expressed goal of performing or meeting a goal at a superior level (winning) either in relation to a previous performance level (one player game) or in relation to the performance levels of other players.   Success in the activity requires use of subject matter in some way.

Educational simulation. A computer program that models some phenomenon or activity and is designed to have participants learn about the phenomenon or activity through interaction with it.   Participants usually have a defined role in the simulation.

Microworld.   An interactive, exploratory learning environment of a small subset of a domain that is immediately understandable by a user and also intrinsically motivating to the user.   A microworld can be changed and modified by the user in order to explore the domain and to test hypotheses about the domain.

References

Barab, S. A., Evans, M. A., & Baek, E. (2003). Activity theory as a lens for characterizing the participatory unit. In D. Jonassen (Ed.), Handbook of research for educational communications and technology (2nd ed., pp. 199-214). Mahwah, NJ: Lawrence Erlbaum Associates.

Berliner, D. C. (2002). Educational research: The hardest science of all. Educational Researcher, 31(8), 18-20.

Brown, A. L. (1992). Design experiments:   Theoretical and methodological challenges in creating complex interventions in classroom settings. The Journal of the Learning Sciences, 2(2), 141-178.

Clements, D. H., & Gullo, D. F. (1984). Effects of computer programming on young children's cognition. Journal of Educational Psychology, 76(6), 1051-1058.

Cobb, P., Confrey, J., diSessa, A., Lehrer, R., & Schauble, L. (2003). Design experiments in educational research. Educational Researcher, 32(1), 9-13.

Collins, A. (1999). The changing infrastructure of education research. In E. C. Lagemann & L. B. Shulman (Eds.), Issues in educational research:   Problems and possibilities (pp. 289-298). San Francisco: Jossey-Bass.

Cuban, L. (2001). Oversold and underused:   Computers in the classroom. Cambridge, MA: Harvard University Press.

Cuban, L., Kirkpatrick, H., & Peck, C. (2001). High access and low use of technologies in high school classrooms:   Explaining an apparent paradox. American Educational Research Journal, 38(4), 813-834.

de Jong, T., & van Joolingen, W. R. (1998). Scientific discovery learning with computer simulations of conceptual domains. Review of Educational Research, 68(2), 179-201.

Dempsey, J., Lucassen, B., Gilley, W., & Rasmussen, K. (1993-1994). Since Malone's theory of intrinsically motivating instruction:   What's the score in the gaming literature? Journal of Educational Technology Systems, 22(2), 173-183.

Dick, W., Carey, L., & Carey, J. O. (2001). The systematic design of instruction (5th ed.). New York: Longman.

diSessa, A. (1997). Twenty reasons why your should use Boxer (instead of Logo). In M. Turcsányi-Szabó (Ed.), Learning & Exploring with Logo: Proceedings of the Sixth European Logo Conference, Budapest, Hungary (pp. 7-27).

diSessa, A. (2000). Changing minds:   Computers, learning, and literacy. Cambridge, MA: The MIT Press.

diSessa, A., & Abelson, H. (1986). Boxer:   A reconstructible computational medium. Communications of the ACM, 29(9), 859-868.

diSessa, A., Abelson, H., & Ploger, D. (1991). An overview of Boxer. Journal of Mathematical Behavior, 10, 3-15.

diSessa, A., Hoyles, C., Noss, R., & Edwards, L. D. (Eds.). (1995). Computers and exploratory learning. New York: Springer.

Edwards, L. D. (1995). Microworlds as representations. In A. A. diSessa, C. Hoyles, R. Noss & L. D. Edwards (Eds.), Computers and exploratory learning (pp. 127-154). New York: Springer.

Erickson, F., & Gutierrez, K. (2002). Culture, rigor, and science in educational research. Educational Researcher, 31(8), 21-24.

Feuer, M. J., Towne, L., & Shavelson, R. J. (2002). Scientific culture and educational research. Educational Researcher, 31(8), 4-14.

Gee, J. P. (2003). What video games have to teach us about learning and literacy. New York: Palgrave MacMillan.

Gentner, D., & Stevens, A. (Eds.). (1983). Mental models. Hillsdale, NJ: Lawrence Erlbaum Associates.

Gredler, M. E. (1996). Educational games and simulations:   A technology in search of a (research) paradigm. In D. Jonassen (Ed.), Handbook of research for educational communications and technology (pp. 521-540). Washington, DC: Association for Educational Communications and Technology.

Gredler, M. E. (2003). Games and simulations and their relationships to learning. In D. Jonassen (Ed.), Handbook of research for educational communications and technology (2nd ed., pp. 571-581). Mahwah, NJ: Lawrence Erlbaum Associates.

Harel, I., & Papert, S. (1990). Software design as a learning environment. Interactive Learning Environments, 1, 1-32.

Harel, I., & Papert, S. (1991). Software design as a learning environment. In I. Harel & S. Papert (Eds.), Constructionism (pp. 41-84). Norwood, NJ: Ablex.

Horwitz, P. (1999). Designing computer models that teach. In W. Feurzeig & N. Roberts (Eds.), Modeling and simulation in science and mathematics education (pp. 179-196). New York: Springer-Verlag.

Jih, H. J., & Reeves, T. C. (1992). Mental models:   A research focus for interactive learning systems. Educational Technology Research & Development, 40(3), 39-53.

Johnson, R. B., & Onwuegbuzie, A. J. (2004). Mixed methods research: A research paradigm whose time has come. Educational Researcher, 33(7), 14-26.

Jonassen, D. (1991). Objectivism versus constructivism: Do we need a new philosophical paradigm? Educational Technology Research & Development, 39(3), 5-14.

Jonassen, D., & Rohrer-Murphy, L. (1999). Activity theory as a framework for designing constructivist learning environments. Educational Technology Research & Development, 47(1), 61-79.

Kafai, Y. (1994). Electronic play worlds:   Children's construction of video games. In Y. Kafai & M. Resnick (Eds.), Constructionism in practice:   Rethinking the roles of technology in learning. Mahwah, NJ: Lawrence Erlbaum Associates.

Kafai, Y. (1995). Minds in play: Computer game design as a context for children's learning. Hillsdale, NJ: Lawrence Erlbaum Associates.

Kafai, Y., Ching, C., & Marshall, S. (1997). Children as designers of educational multimedia software. Computers and Education, 29, 117-126.

Kafai, Y., & Harel, I. (1991). Learning through design and teaching:   Exploring social and collaborative aspects of constructionism. In I. Harel & S. Papert (Eds.), Constructionism (pp. 85-106). Norwood, NJ: Ablex.

Kirriemuir, J., & McFarlane, A. (2004). Literature review in games and learning: A report for NESTA Futurelab. Retrieved September 1, 2004, from http://www.nestafuturelab.org/research/reviews/08_01.htm

Lajoie, S. (Ed.). (2000). Computers as cognitive tools, volume two: No more walls : theory change, paradigm shifts, and their influence on the use of computers for instructional purposes (2nd ed.). Mahwah, N.J.: Lawrence Erlbaum Associates.

Lajoie, S. P., & Derry, S. J. (Eds.). (1993). Computers as cognitive tools. Hillsdale, NJ: Lawrence Erlbaum Associates.

Mayer, R. E. (1989). Models for understanding. Review of Educational Research, 59, 43-64.

Mayer, R. E. (2001). Multimedia learning. Cambridge, UK: Cambridge University Press.

National Research Council. (2002). Scientific research in education. Washington, DC: National Academy Press.

Newman, D. (1990). Opportunities for research on the organizational impact of school computers. Educational Researcher, 19(3), 8-13.

Newman, D. (1992). Formative experiments on the coevolution of technology and the educational environment. In E. Scanlon & T. O’Shea (Eds.), New directions in educational technology (pp. 61-70). New York: Springer-Verlag.

Norman, D. A. (2002). The design of everyday things. New York: BasicBooks.

Olive, J. (1998). Opportunities to explore and integrate mathematics with "The Geometer's Sketchpad" in designing learning environments for developing understanding of geometry and space. In R. Lehrer & D. Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 395-418). Mahwah, NJ: Lawrence Erlbaum Associates.

Paivio, A. (1990). Mental representations:   A dual coding approach (2nd ed.). New York: Oxford University Press.

Paivio, A. (1991). Dual coding theory:   Retrospect and current status. Canadian Journal of Psychology, 45, 255-287.

Papert, S. (1980a). Computer-based microworlds as incubators for powerful ideas. In R. Taylor (Ed.), The computer in the school:   Tutor, tool, tutee (pp. 203-210). New York: Teacher's College Press.

Papert, S. (1980b). Mindstorms:   Children, computers, and powerful ideas. New York: BasicBooks.

Papert, S. (1987). Computer criticism vs. technocentric thinking. Educational Researcher, 16(1), 22-30.

Pea, R., & Kurland, M. (1984). On the cognitive effects of learning computer programming. New Ideas in Psychology, 2, 1137-1168.

Pellegrini, A. D. (Ed.). (1995). The future of play theory:   A multidisciplinary inquiry into the contributions of Brian Sutton-Smith. Albany, NY: State University of New York Press.

Penner, D. E. (2000/2001). Cognition, computers, and synthetic science:   Building knowledge and meaning through modeling. Review of Research in Education, 25, 1-35.

Poole, S. (2000). Trigger happy:   Videogames and the entertainment revolution. New York: Arcade.

Randel, J. M., Morris, B. A., Wetzel, C. D., & Whitehill, B. V. (1992). The effectiveness of games for educational purposes:   A review of recent research. Simulation and gaming, 23, 261-276.

Resnick, M. (1994). Turtles, termites, and traffic jams. Cambridge, MA: MIT Press.

Richey, R. C., & Nelson, W. A. (1996). Developmental research. In D. Jonassen (Ed.), Handbook of research for educational communications and technology (pp. 1213-1245). Washington, DC: Association for Educational Communications and Technology.

Rieber, L. P. (1990). Using computer animated graphics in science instruction with children. Journal of Educational Psychology, 82, 135-140.

Rieber, L. P. (1991). Animation, incidental learning, and continuing motivation. Journal of Educational Psychology, 83, 318-328.

Rieber, L. P. (1992). Computer-based microworlds:   A bridge between constructivism and direct instruction. Educational Technology Research & Development, 40(1), 93-106.

Rieber, L. P. (1996a). Animation as feedback in a computer-based simulation:   Representation matters. Educational Technology Research & Development, 44(1), 5-22.

Rieber, L. P. (1996b). Seriously considering play:   Designing interactive learning environments based on the blending of microworlds, simulations, and games. Educational Technology Research & Development, 44(2), 43-58.

Rieber, L. P. (2003). Microworlds. In D. Jonassen (Ed.), Handbook of research for educational communications and technology (2nd ed., pp. 583-603). Mahwah, NJ: Lawrence Erlbaum Associates.

Rieber, L. P., Boyce, M., & Assad, C. (1990). The effects of computer animation on adult learning and retrieval tasks. Journal of Computer-Based Instruction, 17(2), 46-52.

Rieber, L. P., Davis, J., Matzko, M., & Grant, M. (2001, April). Children as multimedia critics: Middle school students' motivation for and critical analysis of educational multimedia designed by other children: Paper presented at the annual meeting of the American Educational Research Association, Seattle.

Rieber, L. P., & Kini, A. (1995). Using computer simulations in inductive learning strategies with children in science. International Journal of Instructional Media, 22(2), 135-144.

Rieber, L. P., Luke, N., & Smith, J. (1998). Project KID DESIGNER:   Constructivism at work through play. Meridian:   Middle School Computer Technology Journal, 1(1). Retrieved May 19, 2004 from http://www.ncsu.edu/meridian/archive_of_meridian/jan98/index.html.

Rieber, L. P., & Noah, D. (1997, March). Effect of gaming and graphical metaphors on reflective cognition within computer-based simulations. Paper presented at the annual meeting of the American Educational Research Association, Chicago.

Rieber, L. P., Noah, D., & Nolan, M. (1998, April). Metaphors as Graphical Representations within Open-Ended Computer-Based Simulations. Paper presented at the annual meeting of the American Educational Research Association, San Diego.

Rieber, L. P., & Parmley, M. W. (1995). To teach or not to teach? Comparing the use of computer-based simulations in deductive versus inductive approaches to learning with adults in science. Journal of Educational Computing Research, 13(4), 359-374.

Rieber, L. P., Smith, M., Al-Ghafry, S., Strickland, W., Chu, G., & Spahi, F. (1996). The role of meaning in interpreting graphical and textual feedback during a computer-based simulation. Computers and Education, 27(1), 45-58.

Rieber, L. P., Tzeng, S., & Tribble, K. (2004). Discovery learning, representation, and explanation within a computer-based simulation:   Finding the right mix. Learning and Instruction, 14, 307–323.

Roschelle, J., & Jackiw, N. (2000). Technology design as educational research: Interweaving imagination, inquiry and impact. In A. Kelley & R. Lesh (Eds.), Handbook of Research design in mathematics & science education (pp. 777–797). Mahwah, NJ: Lawrence Erlbaum Associates.

Roschelle, J., Kaput, J., & Stroup, W. (2000). SimCalc: Accelerating student engagement with the mathematics of change. In M. J. Jacobson & R. B. Kozma (Eds.), Learning the sciences of the 21st century: Research, design, and implementing advanced technology learning environments (pp. 47-75). Hillsdale, NJ: Lawrence Erlbaum Associates.

Sadoski, M., & Paivio, A. (2001). Imagery and text: A dual coding theory of reading and writing. Mahwah, NJ: Lawrence Erlbaum Associates.

Salomon, G., Perkins, D. N., & Globerson, T. (1991). Partners in cognition:   Extending human intelligence with intelligent technologies. Educational Researcher, 20(3), 2-9.

Sutton-Smith, B. (1997). The ambiguity of play. Cambridge, Mass: Harvard University Press.

White, B. Y. (1984). Designing computer games to help physics students understand Newton's laws of motion. Cognition and Instruction, 1(1), 69-108.

White, B. Y. (1992). A microworld-based approach to science education. In E. Scanlon & T. O’Shea (Eds.), New directions in educational technology (pp. 227-242). New York: Springer-Verlag.

White, B. Y. (1993). ThinkerTools:   Causal models, conceptual change, and science education. Cognition and Instruction, 10(1), 1-100.

White, B. Y., & Frederiksen, J. R. (1998). Inquiry, modeling, and metacognition:   Making science accessible to all students. Cognition and Instruction, 16(1), 3-118.

White, B. Y., & Frederiksen, J. R. (2000). Technological tools and instructional approaches for making scientific inquiry accessible to all. In M. J. Jacobson & R. B. Kozma (Eds.), Learning the sciences of the 21st century: Research, design, and implementing advanced technology learning environments (pp. 321-359). Hillsdale, NJ: Lawrence Erlbaum Associates.

White, B. Y., & Horowitz, P. (1987). ThinkerTools: Enabling children to understand physical laws (No. 6470). Cambridge, MA: Bolt, Beranek, and Newman, Inc.

White, B. Y., & Schwarz, C. V. (1999). Alternative approaches to using modeling and simulation tools for teaching science. In W. Feurzeig & N. Roberts (Eds.), Modeling and simulation in science and mathematics education (pp. 226-256). New York: Springer-Verlag.

Zhao, Y., & Frank, K. A. (2003). Factors affecting technology uses in schools:   An ecological perspective. American Educational Research Journal, 40(4), 807-840.